Let’s just start from Bragg scattering, as highlighted in our recent article. The benefits of being able to finely resolve these Bragg peaks are numerous. However, diffraction patterns are much more than a set of peaks. They are continuous functions, and some of the scattering intensities coming from our structure are not located within those peaks. Sometimes, there are no peaks at all!

This is where total scattering comes into play. Rather than considering the diffraction pattern as a set of discrete peaks arising from an infinite perfect lattice, we consider it from the atomic perspective via sets of correlation functions that arise from the relative positions of all atoms in the ensemble. This allows us to make fewer assumptions about the structure, especially when it comes to periodicities and crystallographic symmetries… although we can build those assumptions back in. How do we leverage that perspective to improve the information utility of the diffraction pattern? We optimize our measurement to capture the full information as best as possible:

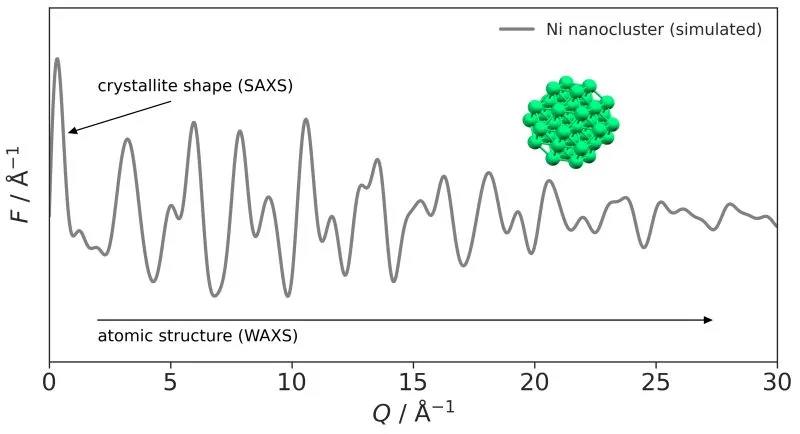
• collect the diffraction pattern over as wide of a Q-range as possible. This allows us to capture information about the crystallite shape and size from the small-angle (or low-Q) scattering (SAXS) and an extremely high spatial resolution of the atomic structuring from the wide-angle (or high-Q) scattering (WAXS) — see for instance the image showing the scattering regimes for a model nanocluster of nickel, which is used in catalysis.
• collect the data with enhanced statistics. It is critical that the low intensitiy, diffuse parts are captured well above the noise level; we also take and subtract careful background measurements to account for and remove all non-sample contributions;
• depending on the further details of the analysis, we may perform various normalization steps that improve the sensitivity to certain features of the structure.

With all of that, we can augment our view of a material. Why is this important?

• measurements with higher Q increase our accuracy in assessing bond lengths and molecular conformations
• we are more flexible in the type of models we use to leverage information from certain frequency bands
• we are more flexible in the type of models we use to leverage information from certain frequency bands
• we can better represent the effects of structural defects, disorder, and finite dimensions on the

diffraction by accounting for them discretely in more detailed atomic models.